
Activities to Practice Angle Congruence by ASA and AAS It also includes short exercises to decide which postulate to use for a set of triangles.

It contains simple explanations of the two, as well as their differences. To illustrate the difference between triangle congruence by ASA and AAS, play this video. For instance, use this video by Khan Academy to introduce triangle congruence by ASA and AAS.
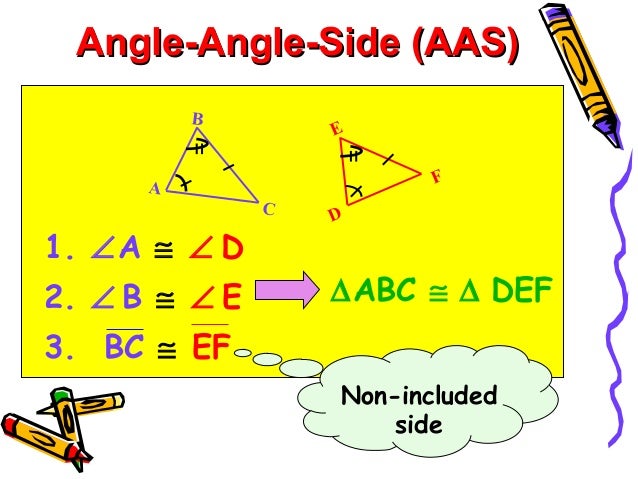
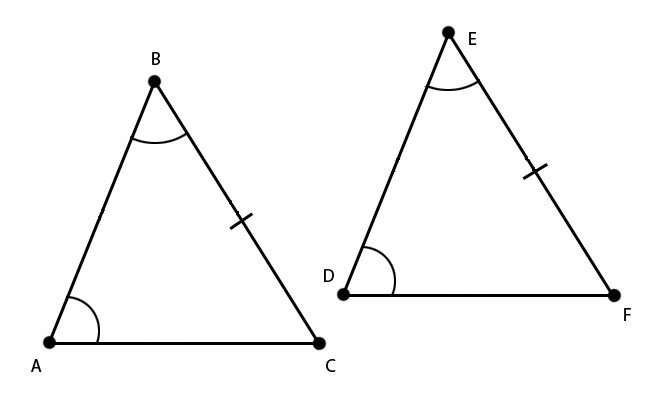
If you have the technical means in your classroom, enrich your lesson on triangle congruence by ASA and AAS by including multimedia material, such as videos. Therefore, there is triangle congruence by angle-angle-side or AAS. Why are these two triangles congruent by the AAS theorem? We notice that we have two congruent angles, and the side is outside or not included between these two angles. Present an example of two triangles that are congruent by the AAS postulate on the whiteboard, such as the following two triangles:Īsk students to reflect again. We call this triangle congruence by AAS or angle-angle-side. Point out that if two angles and their non-included side of one triangle are congruent to the corresponding two angles and their non-included side of another triangle, the two triangles are congruent. Now you can move on to explain triangle congruence by AAS. Why are these two triangles congruent by the ASA theorem? We notice that the congruent side is in between the two congruent angles, that is, there is triangle congruence by angle-side-angle or ASA. Present an example of two triangles that are congruent by the ASA postulate on the whiteboard, such as the following two triangles:Īsk students to reflect. We call this triangle congruence by ASA or angle-side-angle. What Is Triangle Congruence by ASA and AAS?Įxplain to students that if two angles and their included side of one triangle are congruent to the two angles and their included side of another triangle, then the two triangles are said to be congruent. While congruent figures have the same shape and size, similar figures have the same shape, but different sizes. You can also remind students of the difference between congruent and similar figures. Point out that these two figures are congruent because we can easily observe that they have the same shape (they are both pentagons) and they also have the same size. Draw an example on the whiteboard of two figures that are congruent, such as the figures below: Remind students that we define congruent figures as figures that have the same shape and the same size.Īlso, add that the corresponding angles of two congruent figures are equal and the corresponding sides are equal. You can start your lesson on triangle congruence by ASA and AAS by providing a brief review of what congruent figures are.
#AAS GEOMETRY HOW TO#
How to Teach Triangle Congruence by ASA and AAS Review Congruent Figures If you’re teaching this topic and wondering how to make these lessons accessible and exciting for your students – we’ve got you covered! Use the teaching strategies that we share in this article and make the class atmosphere as inviting as it gets! More specifically, they learn how to prove triangles are congruent using ASA and AAS. Use to draw a ray from point B through point A' that were created by the angle tool.After students familiarize themselves with congruent figures, they move on to triangle congruence by ASA and AAS.Use to draw an angle at point B. If requested for the angle size type in 30 degrees.But you do know that the sum of the interior angles of a triangle is 180 degrees. The problem is you cannot draw the next angle as you do not know the length of side AC.Use to draw a ray from point A through point B' that were created by the angle tool.Lastly you need to select clockwise or counterclockwise. The direction of movement is from the line in a clockwise or counterclockwise direction. ( Hint: Always click last on the point where you want the angle.) If requested for the angle size type in 40 degrees. Use to draw segment AB and if you are requested to give the length type in 5.You need to draw a triangle with side AB=8cm an angle CAB of 40 degrees and angle BCA of 110 degrees. Try to do this in the "Applet" below Now you try to draw a triangle congruent to the previous one


 0 kommentar(er)
0 kommentar(er)
